

Nella letteratura crittografica si trovano occasionali menzioni di una cifra delle caselle usata dai Veneziani alla fine del Cinquecento. Per esempio David Kahn nel suo monumentale Codebreakers a pag. 117 riferisce un curioso episodio, tratto del Baschet*: François Viète, il famoso matematico francese, era anche un eccellente crittoanalista famoso per aver sistematicamente decrittato i nomenclatori usati dagli spagnoli, e si era anche vantato di saper decrittare i cifrati veneziani; su questo episodio vedi la pagina François Viete e la cifra delle caselle.
Altri autori come Paolo Preto menzionano questa misteriosa cifra delle caselle, ma senza spiegare di cosa si trattasse. Insomma questa cifra delle caselle era un oggetto alquanto misterioso.

|
| Il dispaccio cifrato di Alberto Badoer. Archivio di Stato di Venezia, CCX, dispacci degli ambasciatori, b. 13 Germania c. 155. È vietato ogni uso a scopo di lucro. |
Nel dicembre 2018 il prof. Elio Canestrelli, già docente di matematica all'Università Ca' Foscari di Venezia, mi propose alcuni cifrati trovati nell'Archivio di Stato di Venezia, in particolare un dispaccio al Consiglio di Dieci dell'ambasciatore veneziano a Praga*, Alberto Badoer. Nonostante fosse presente la decifra di cancelleria non si riusciva a ricostruire il cifrario.
Mi cimentai subito nell'impresa. Indubbiamente mettendo in parallelo il cifrato e il chiaro non si cavava nulla, ipotizzando che si trattasse del solito nomenclatore veneziano, con alfabeto, sillabario, dizionario. La cosa curiosa era che le cifre erano disposte in modo molto ordinato su 21 colonne raggruppate a tre a tre, sette per tre, ventuno colonne, cosa che faceva pensare all'uso di una griglia. La prima idea che mi venne fu quindi quella che il cifrato fosse stato sottoposto a una trasposizione, forse appunto con una griglia, in sostanza che si trattasse di una sovracifratura. Ma anche l'ipotesi della trasposizione non portava a nessun risultato plausibile.
|
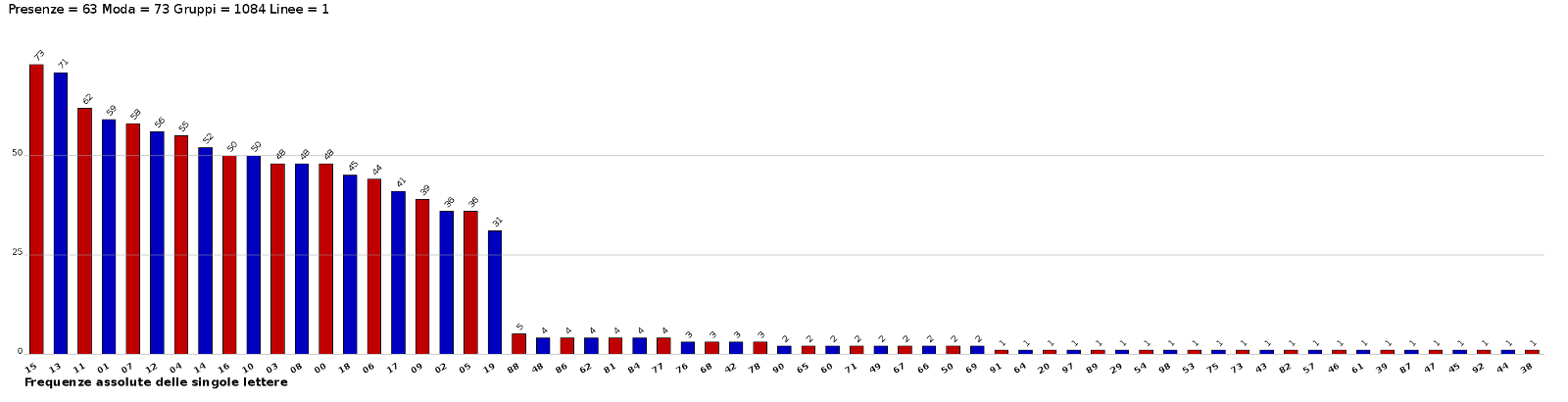
| Distribuzione delle frequenze del messaggio di Alberto Badoer. Visibilissimo il gap tra le 20 cifre e le altre 60. |
In questi casi il primo passo da farsi è sempre un'analisi delle frequenze. Il diagramma a lato ordinato per frequenze decrescenti ha un andamento singolare. I primi 20 numeri hanno una frequenza molto elevata a confronto con i rimanenti tutti a livelli minimi. Ovvia la conclusione che i primi venti numeri rappresentino le venti lettere dell'alfabeto italiano*, e i rimanenti 60 parole di un piccolo dizionario. Nell'archivio veneziano si conservano molte cosiddette cifre piccole, piccole perché con due cifre si possono rappresentare al massimo 100 lettere o gruppi, a differenza delle cifre grandi a tre numeri o una lettera e due numeri con le quali si possono cifrare centinaia di lettere, sillabe e parole.
Quello che appariva anomalo era però l'andamento della distribuzione delle 20 lettere; troppo uniforme, troppo poca differenza tra le frequenze più alte e quelle più basse. Un andamento incompatibile con l'ipotesi di una cifra monoalfabetica, e quindi anche con la trasposizione che non può modificare le frequenze; viceversa l'andamento ricorda molto quello di una cifra polialfabetica.
Dunque un nomenclatore, cifra piccola, e al tempo stesso un polialfabetico? Emerge di nuovo l'ipotesi di una sovracifratura.

|
| La grata Germania. Archivio di Stato di Venezia, CX - Cifre, chiavi e scontri di cifra ... b.4, reg. 8. È vietato ogni uso dell'immagine a scopo di lucro. |
La mia fortuna fu che da mesi stavo studiando i cifrati e i cifrari custoditi all'archivio veneziano, e che poche settimane prima avevo notato una serie di griglie su fogli sciolti e anche un libro contenente pagine con finestrelle ritagliate, che a memoria avevano uno schema simile a quello dei cifrati di Alberto Badoer.
Ritrovai subito le foto che avevo fatto a quelle griglie; ogni pagina conteneva 8 finestrelle per riga e ogni finestrella aveva tre numeri compresi tra 0 e 19 scritti sopra; otto per tre ventiquattro. Mi ero a suo tempo chiesto cosa significassero quei numeri, forse una trasposizione, come altre trovate in archivio. Ma ora l'idea della sovracifratura polialfabetica suggeriva la soluzione giusta: probabilmente i numeri andavano sommati o sottratti a quelli ricavati da un cifrario di base, quindi una sovracifratura tipo Vigenere con un verme molto lungo (tutti i numeri di una pagina).
Mi misi subito al lavoro, le griglie erano rilegate in un libretto, ve ne erano quattro, una denominata Germania (Sacro Romano Impero), una Francia e Savoia, una Spagna e una Costantinopoli e isole. Provai subito a mettere a confronto la prima grata con il cifrato di Badoer, sommando numero a numero e confrontando con la decifra, fu facile ricostruire il cifrario di base, nel quale riconobbi la cosiddetta "zifra piccola" un nomenclatore con alfabeto di venti lettere ognuna con un omofono stranamente spostato di 20, per esempio la lettera A si cifra con 16 ma anche con 36, e di un dizionario di 60 parole.
Ormai tutti i pezzi del puzzle andavano a posto. In altra pagina pubblico i dettagli crittografici. Su un libro nella stessa busta di quello con le griglie, trovai anche la "ziffra piccola" e in alto vi era scritto leggibilmente: "da usarsi con le caselle". Il mistero della cifra delle caselle era finalmente risolto. Nella prima pagina del libro viene riportato un verbale di una riunione del Consiglio di Dieci, deve veniva anche menzionato l'inventore della cifra, Hieronimo di Franceschi, segretario del Senato, che in altri documenti viene definito l'uomo chiave della crittografia veneziana in quegli anni.
Finora i primi esempi di sovracifratura conosciuti risalivano alla fine del XVIII secolo, e la sovracifratura divenne pratica comune nell'Ottocento. Questa cifra delle caselle sarebbe quindi ora il primo esempio di sovracifratura nella storia delle crittografia, in anticipo di due secoli. Affermazione da prendere ovviamente con qualche cautela; nella storia è sempre difficile stabilire chi realmente inventò o scoprì qualcosa per primo. In Europa ci sono centinaia di archivi con messaggi cifrati ed è possibile che prima o poi si scoprano esempi di sovracifratura precedenti a questa invenzione del Franceschi.
Va aggiunto che dopo il Franceschi, il suo amico/rivale Pietro Partenio inventò altri sistemi sovracifrati ancora più ingegnosi, dettagliatemante descritti in un libricino e in altri documenti custoditi nell'archivio veneziano. Prossimamente su queste pagine.
L'idea di sovracifratura è certo molto più antica se è vero che Al-Kindi già nel IX secolo accennava alla possibilità di combinare più cifre, ma senza fornire alcun dettaglio o esempio*. Queste di Franceschi e Partenio sono per ora i primi esempi di sovracifratura ben documentata ed effettivamente usata.
Nell'archivio veneziano è conservato il verbale della riunione del CX il 5 giugno 1595, ASVE CX Deliberazioni (Parti) secrete filza 26. Ecco il testo della deposizione di Mocenigo davanti al consiglio.
Io mi trouaua a Tours doue ragionando un giorno con Mons. de Viet mi uenne a dire che erano intercette moltissime lettere scritte in zifra così del Re di Spagna, che andauano et ueniuano, così come dell’Imperatore et altri Principi, le quali lettere erano state leuate et interpretate da lui per la notitia che haueua della materia delle zifre, et mostrando io marauigliarmi di ciò, egli disse lo farò vedere a V.S. in fatto; et mi portò un gran fascio di lettere dei suddetti Principi leuate da lui. Il quale mi aggiunse: Voglio che sappiate anco che io intendo et leuo la uostra zifra; non uoglio creder, diss’io, questo se non lo ueggo, ciò perché io mio trouaua hauere tre sorte di zifra : una ordinaria che io usaua, l’altra d’un’altra sorta la quale non si adoperaua, et la terza delle caselle; mi mostrò di hauer intelligenza della prima; onde io per penetrar più addentro in questo fatto sì importante, li dissi: intendete uoi anco forse la zifra nostra delle caselle? Egli rispose: In quella bisogna far salti; uolendo inferire che non la intendeua e non interrottamente, et pregatolo io à farmi uedere delle lettere nostre leuate da ui, disse che lo farebbe; nondimeno poi se ne andò ma senza tornare a parlarmi; et non lo uidi più. Ma però è da tener per fermo et per quanto mi haueua detto et mostrato delle zifre di altri Principi et per quanto haueua ragionato meco in questa materia, che le nostre zifre non sono così difficili a leuarsi, come si stima. La qual cosa hauendo io conseruata bene alla memoria per esser di quella importanza che è noto a VV.SS.Ill.me subito tornato ho uoluto discarcarmene la coscientia con farlo sapere, sicome anco al presente acciò ui sia fatta la prouisione che parerà necessaria alla prudentia di VV. SS. Ill.me.