Questa cifra, detta anche rete, fu ideata dal crittologo Horst Feistel nel 1973; si tratta di un cifrario che mescola trasposizioni e sostituzioni a livello di bit, non di carattere. Non ha avuto di per sé applicazioni pratiche, ma è stato usato come componente fondamentale per costruire cifrari reali, il più noto di tutti essendo il DES.

Il testo chiaro deve essere prima di tutto tradotto in una sequenza di bit secondo un qualche codice binario, tipicamente l'ASCII. Per esempio il messaggio chiaro "Chiedo conferma" usando il codice ASCII si traduce nella seguente sequenza di bit:

È poi necessaria una chiave segreta K di N bit (64, 128, 256 bit o altro); per semplicità, ma senza perdere in generalità, prenderemo come esempio una chiave di soli 8 bit divisa in due sottochiavi da 4 bit: 0100 1110.

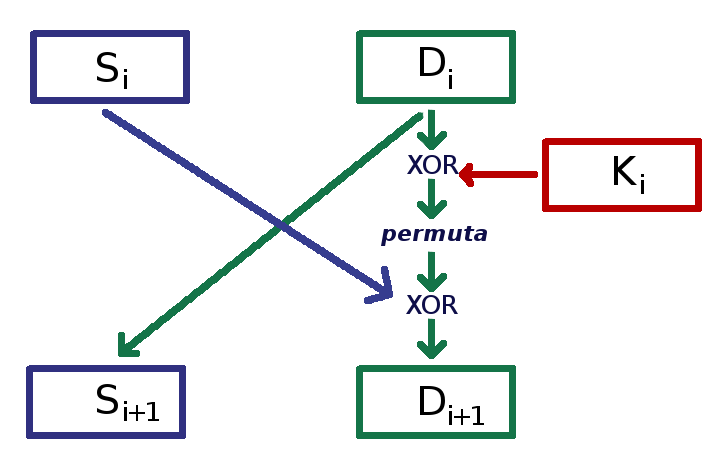
Il metodo si articola in una serie di cicli che consistono nel dividere in due parti uguali il blocco da cifrare e nello scambiarli; uno dei due blocchi viene anche sottoposto a un misto di permutazioni e sostituzioni usando la sottochiave, come nello schema qui accanto, dove S_i, D_i, K_i sono i blocchi sinistro e destro e la sottochiave dell'i-esimo ciclo, S_i+1, D_i+1 quelli del ciclo successivo.

Vediamo in maggior dettaglio il metodo usando come esempio solo il primo blocco di 8 bit da cifrare: 0100 0011.

Questa sequenza viene divisa in due parti uguali: sinistra S='0100' e destra D='0011'.

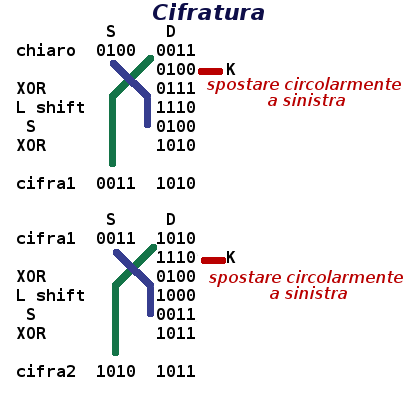
D diventa la S del prossimo ciclo (in simboli S_i+1 ← D_i); la D del prossimo ciclo (D_i+1)si ottiene con un misto di trasposizioni e sostituzioni: si calcola l'addizione XOR tra la sottochiave K_i e D_i, il risultato viene sottoposto ad una permutazione dei bit (la funzione risultante da XOR e permuta si scrive di solito f(K, D)); nell'esempio semplificato qui sotto la permutazione consiste nello spostare circolarmente a sinistra i bit (left shift); il risultato viene poi sommato ad S_i sempre con uno XOR.

Ripetendo molte volte questa trasformazione si ottiene una sequenza di bit pressochè casuale, che dovrebbe nascondere del tutto ogni caratteristica statistica del testo cifrato.

In definitiva una rete di Feistel prevede tre parametri variabili: la lunghezza della chiave K, la dimensione del blocco di bit, il numero di iterazioni del ciclo appena descritto. Inoltre va definita la funzione F(K, D).

Tanto più grandi sono questi parametri, tanto maggiore la sicurezza, ma a scapito della complessità e della velocità di esecuzione.

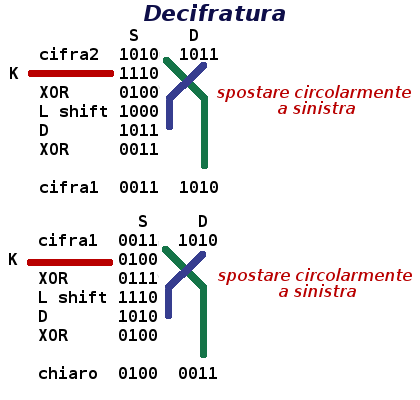
La decifra avviene con la stessa procedura utilizzando le sottochiavi in ordine inverso come illustrato nella figura accanto. In sostanza l'algoritmo di decifratura è identico a quello di cifratura e questo semplifica la realizzazione del software.